No Rules Rules
구간 합 구하기 5 (feat. 백준, 11660번) 본문
구간 합 구하기 5
https://www.acmicpc.net/problem/11660
11660번: 구간 합 구하기 5
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net
// woohyeon.kim
// https://www.acmicpc.net/problem/11660
#include <iostream>
using namespace std;
int main() {
ios::sync_with_stdio(false), cin.tie(NULL);
register int N, M;
int dp[1025][1025] = { 0 };
cin >> N >> M;
for (register int x = 1, y, v; x <= N; ++x)
for (y = 1; y <= N; ++y)
cin >> v, dp[x][y] = v + dp[x - 1][y] + dp[x][y - 1] - dp[x - 1][y - 1];
for (register int i = 0, x1, y1, x2, y2; i < M; ++i) {
cin >> x1 >> y1 >> x2 >> y2;
auto& total = dp[x2][y2]; // 0,0 ~ x2,y2까지의 총합
auto& left_section = dp[x2][y1 - 1]; // 0,0 ~ x2,y1-1까지의 총합
auto& up_section = dp[x1 - 1][y2]; // 0,0 ~ x1-1,y1까지의 총합
auto& intersection_section = dp[x1 - 1][y1 - 1]; // 0,0 ~ x1-1, y1-1까지의 총합
cout << total - left_section - up_section + intersection_section << "\n";
}
return 0;
}
// *&)*@*x1,y1 ~ x2,y2로 for문을 돌리면서 더하면 시간 초과가 납니다. (해봤습니다.)
그래서 dp 형태로 풀이를 하였습니다.
일단 dp를 만드는 방법입니다.
| 1 | 2 |
| 3 | 4 |
이러한 2x2 행렬이 있다고 하면 해당 행렬의 누적합 dp는 아래와 같습니다.
| 1 | 3 |
| 4 | 10 |
(1,1) + (1,2) 는 1 + 2 = 3 입니다. (1,1) + (2,1) 은 1 + 3 = 4 입니다.
(1,1) + (1,2) + (2,1) + (2,2) 는 1 + 2 + 3 + 4 = dp(1,2) + dp(2,1) + (2,2) - dp(1,1) = 10 입니다.
dp(1,1)을 빼는 이유는 dp(1,2)와 dp(2,1)에서 중복되어 계산되었기 때문입니다.
이제 dp를 모두 구했으니 (x1,y1) ~ (x2,y2)의 합을 구해보겠습니다.
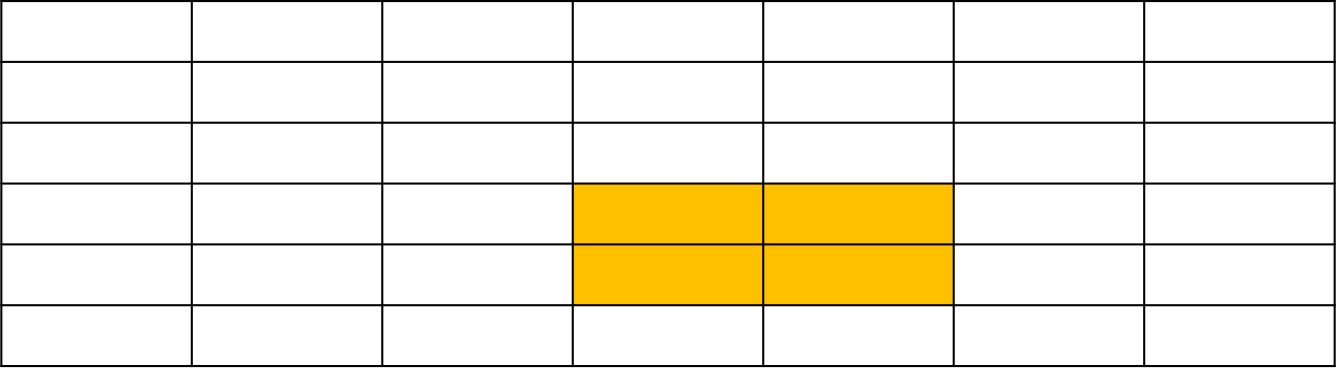
위 주황색 부분이 (x1,y1) ~ (x2,y2) 구역이라고 한다면, dp에서 dp(x2,y2)는
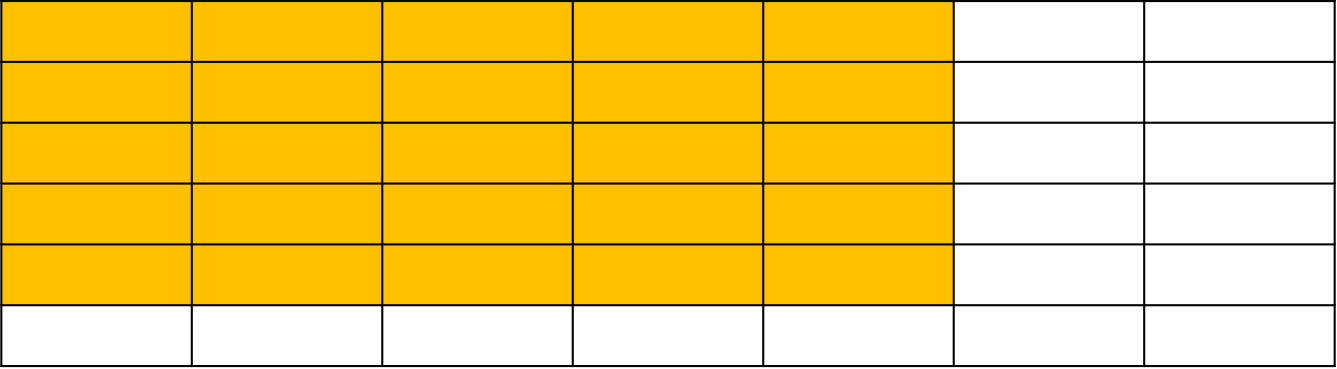
(0,0) ~ (x2,y2) 의 총합과 같습니다. 따라서 dp(x2,y2)는 (x1,y1) 이전의 영역이 모두 포함된 상태입니다. 따라서
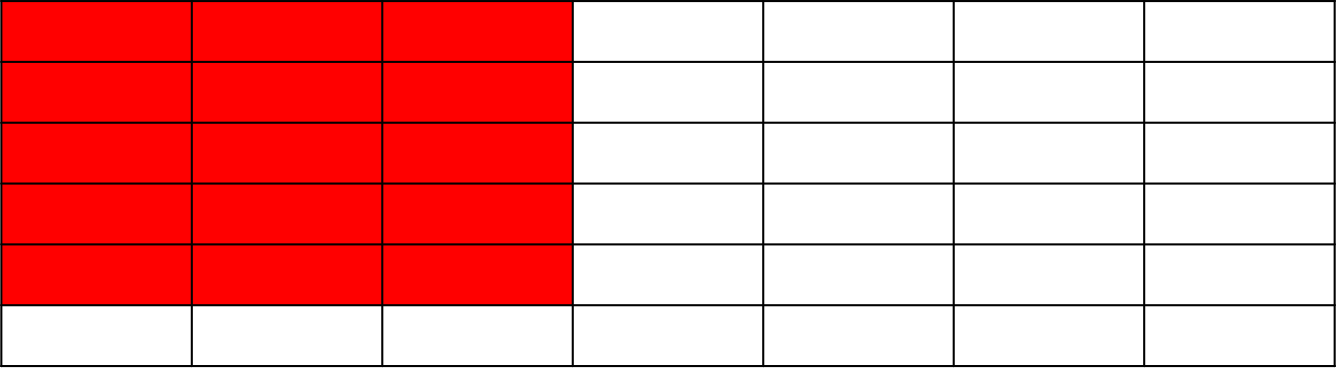
(x2,y1) 기준 좌측 영역의 총합을 빼주어야 합니다. 여기서 총합은 dp(x2, y1 - 1)의 값이 됩니다. 또한

(x1,y2) 기준 상단 영역의 총합도 빼주어야 합니다. 여기서 총합은 dp(x1 - 1, y2)의 값이 됩니다. 그리고 여기서 빨강색 영역과 초록색 영역에서 중복되어 연산된 영역이 존재합니다.
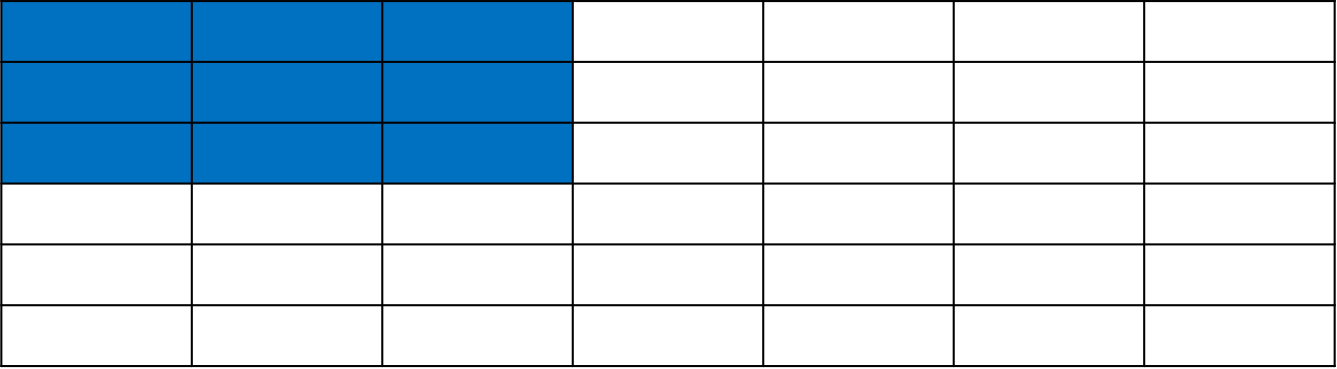
바로 위 파랑색 영역입니다. 파랑색 영역의 총합은 dp(x1 - 1, y1 - 1)의 값이 됩니다. 따라서 구하고자 하는 (x1,y1) ~ (x2,y2)의 총합은 dp(x2,y2) - dp(x2, y1 - 1) - dp(x1 - 1, y2) + dp(x1 - 1, y1 - 1)이 됩니다.
'생활 > 코테' 카테고리의 다른 글
| 약수의 개수와 덧셈 (feat. 프로그래머스, 77884번) (0) | 2022.07.26 |
|---|---|
| 동물원 (feat. 백준, 1309번) (0) | 2022.07.26 |
| 전깃줄 (feat. 백준, 2565번) (0) | 2022.07.26 |
| [1차] 뉴스 클러스터링 (feat. 프로그래머스, 17677번) (0) | 2022.07.26 |
| 주사위 굴리기 2 (feat. 백준, 23288번) (0) | 2022.07.25 |

